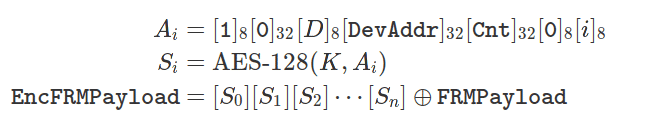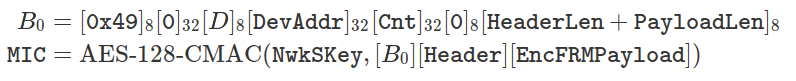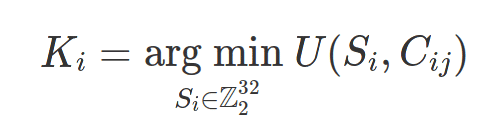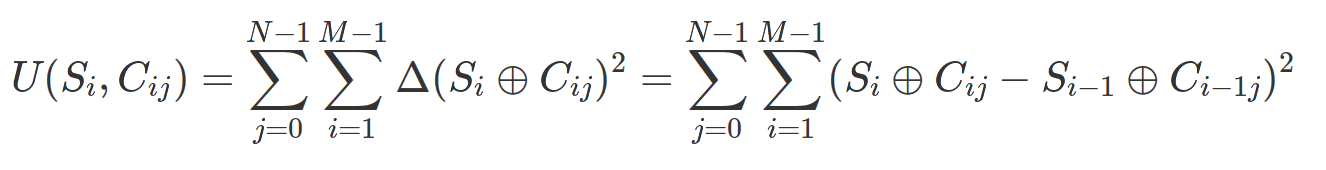LoRaWAN 1.0, vulnerabilities and backward compatibility in version 1.1
Table of Contents
To understand the security improvements introduced in 1.1, it is necessary to have a thorough understanding of the security mechanisms described in LoRaWAN 1.0.
LoRaWAN Security
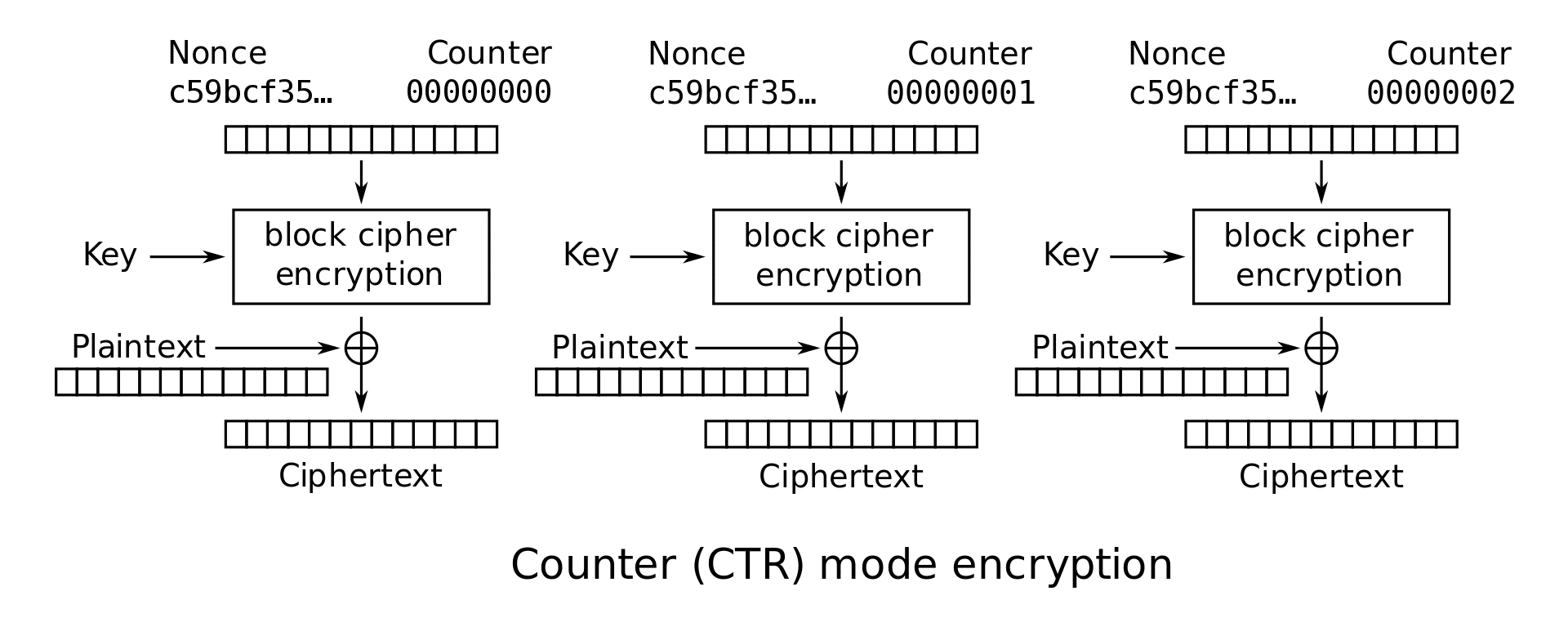
As described in the previous article, whatever the activation procedure used, the communication is protected by two AES128 session keys: AppSKey and NwkSKey. These keys are not used to encrypt in block mode but in flow mode, from a variation of the CTR mode (Counter mode) named CCM*.
CTR is a well-known method for converting a block cipher (such as AES128) into a stream cipher. For this purpose, the plain text is divided into blocks of the size accepted by the block cipher and each block of plain text is combined (e.g. bit by bit using XOR) with the block resulting from encrypting a block counter and an IV/Nonce from a certain key that is assumed to be secret.
Security in this way is then reduced to proper management of the cryptographic material required to generate the keystream.
CCM* uses CTR mode to encrypt the payload content using the AppSKey, and authenticates the message with a code CMAC based on the NwkSKey. The keystream generator blocks (Ai) are encrypted with a certain key (AppSKey or NwkSKey) depending on the type of the packet, and the result is applied to the 128-bit blocks that make up the payload of the message:
The subscripts indicate the size of each concatenated field in bits. The bytes of fields larger than 8 bits are sorted in little endian mode. The field D (address) is 0 for uplink and 1 for downlink. The counter (Cnt) is the message counter used, depending on the message direction, and is worth 0 at the start of the session. The block counter (i) lists the AES block to which the encryption result applies. The key K is NwkSKey or AppSKey depending on the type of MAC packet involved (control or data respectively).
The resulting message is authenticated using AES-128-CMAC to generate the message integrity code (MIC) using the NwkSKey, regardless of the type of packet. This integrity code is calculated on the header, the payload already encrypted and a certain block B0 concatenated at the beginning of both:
With identical bit order. In both cases, the cryptographic material involved is:
- Frame direction (uplink/downlink).
- Address (32 bits) of the device.
- A message counter expanded to 32 bits (which depending on the frame address can be 16 or 24 bits).
- A 128-bit AES key.
In addition to the lack of end-to-end security mentioned in the previous article, improper handling of this material can compromise communications security. This and other weaknesses are detailed in the Security of LoRaWAN v1. 1 in Backward Compatibility Scenarios article. Dönmez, T.C.; Nigussie, E. Procedia computer science 2018, 134, 51-58. In particular, in version 1.0.2 of the protocol specification, the weaknesses found were as follows:
- Reuse of message counters: as seen above, frames in LoRaWAN 1.0 are encrypted in CTR mode. This method is not inherently insecure. However, a weak key update policy can make it ineffective. When using ABP, the device usually communicates with the network with the message counter reset to its initial value (so the IV is always the same). This leads to a type of plaintext attack called crib dragging which, depending on the knowledge of the structure of the messages, can compromise all communication. Obviously, the more frames are captured, the more likely it is to break this encryption.
- Nonces reuse: during the Join process, there is an exchange of nonces between the end device and the network (called DevNonce and AppNonce), which are used to prevent replay attacks. Because the generation of these nonces is not properly recorded, the reuse of some nonces cannot be completely prevented.
- No Join accept replay protection mechanism: the end device is unable to detect repeated nonces during OTAA, so replays of Join-accept type messages can occur.
- Poor Join request message replay protection: the network server only detects a certain non-specific number N of DevNonces, so an attacker should only wait N messages before replaying a Join request message.
- ACK type messages are not associated with acknowledged messages: in LoRaWAN 1.0.2, acknowledgement messages are not associated with any specific message, which could allow replay attacks.
- Join accept type messages are not associated with Join-requests: there is no way to connect Join requests made in OTAA in LoRaWAN 1.0.2 with their corresponding accept, beyond their temporary occurrence.
- No mechanism for confirmation of security context changes: ‘Security context’ refers to the set of counters and keys required for frame encryption and authentication. When a change in that context occurs, the network server confirms it by its mere presence in an upstream frame (i.e. from the end device). However, the end device has no way of confirming these context changes, and may become disassociated from the network server.
- Without end-to-end protection: and finally, as discussed in the previous entry, because the AppKey is shared by both the network server and the application servers, nothing prevents the network server from intercepting the content of the frames directed to the application servers.
LoRaWAN 1.1 Countermeasures
LoRaWAN 1.1 introduces a number of changes that correct these vulnerabilities in different ways:
- The reuse of counters is corrected by anticipating their overflow (using a new message called Rejoin request) and, in the particular case of ABP, by storing the last value of the counter in non-volatile memory.
- The reuse of nonces is prevented by properly registering the generated nonces, avoiding their reuse.
- The replay of messages of type Join accept is prevented by the end device by keeping a value called JoinNonce_last, with the last JoinNonce generated by the network. If the end device does not see an incremental JoinNonce compared to the JoinNonce_last, it silently discards it.
- The replay of messages of type Join request is prevented by the network by maintaining a value called DevNonce_last, preventing non-incremental DevNonces, in a way equivalent to the previous case.
- The prevention against ack messages not associated with any message is corrected by entering the number of packets received by the other end (based on the FCnt) into the MIC itself, coupling its calculation to its relative position in the communications.
- The association of Join requests with Join accepts is corrected by entering the DevNonce of the corresponding Join request in the MIC calculation of the Join Accept.
- Confirmation of security context changes are corrected by entering additional MAC commands, first to request the change (RekeyInd) and then to confirm it at the other end (RekeyConf).
- And finally, end-to-end protection for OTAA is achieved by providing two different keys for the network (NwkKey) and for the application (AppKey), from which all other keys are derived.
Back to square one
Although these measures are effective when employed individually, they involve changes to the protocol that make it fundamentally incompatible with LoRaWAN 1.0. If a 1.1 device wants to communicate with a 1.0 network, the device must support 1.0. Similarly, if a 1.1 network wants to support 1.0 devices (which are still the majority of the market), it must downgrade to 1.0.
Some of the countermeasures that apply exclusively to key life cycle policies can be used in 1.0 (such as preventing meter reuse). However, this is only possible on the end device side, when the device is 1.1 and the network is 1.0. In contrast, the only thing the network can do is block access to the device when its security status is being reused. We can therefore conclude that the security of a LoRaWAN 1.1 network can only be achieved by ensuring that there are no 1.0 elements in it.
A practical example
One of the most critical failures of LoRaWAN 1.0 concerns the reuse of the keystream, which happens when the value used as IV (the packet counter) in the AES CTR mode is reset. In the case of ABP, this happens when the end device is restarted and does not hold the last counter value. In the case of OTAA, it is when the meters overflow (which is statistically more unlikely). In the particular case of ABP, the characteristics of the encrypted traffic (sensor measurements) make it particularly vulnerable.
To illustrate the extent of this vulnerability, let’s look at a fairly common scenario: a set of simple sensors (humidity, temperature, etc.) managed by a microcontroller, which sends the measurements back to a small LoRa board, using LoRaWAN 1.0/ABP for activation and powered autonomously (either by solar panel or battery).
We can then run continuous traffic monitoring using a device such as the HT-M01, a normal LoRa gateway, controlled through an integrated USB/serial emulator.
The HT-M01 is a device originally conceived for the deployment of LoRaWAN networks, acting as a gateway between the end devices and the rest of the network infrastructure. Without this structure, the HT-M01 acts as a true LoRa sniffer (not necessarily LoRaWAN), redirecting demodulated frames to another host via UDP. These frames and their metadata are encoded in JSON, making it easy to manipulate them from script languages, and look like this:
{"rxpk":[{"tmst":3881858452,"chan":1,"rfch":1,"freq":868.300000,"stat":1,"modu":"LORA","datr":"SF7BW125","codr":"4/5","lsnr":9.5,"rssi":-27,"size":17,"data":"QOGUkACAAAAB5pyQk6nCOeM="}]}
Where the data field is the PHY payload of the captured LoRa frame, encoded in base 64. The other fields specify information such as reception timestamp, modulation, coding rate, signal-to-noise ratio and so on.
The interesting thing about LoRaWAN packages is that, although the payload can be encrypted, the headers are not. These headers are well documented and are distributed as follows:
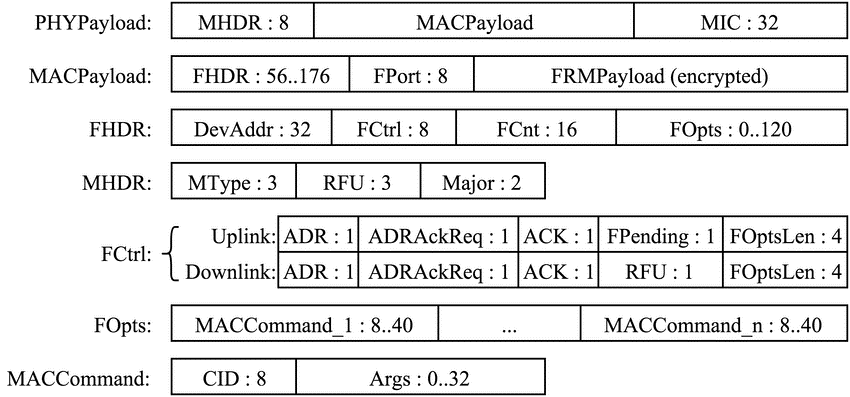 LoRaWAN headers. Source: A Study of LoRa Long Range Low Power Networks for the Internet of Things.
LoRaWAN headers. Source: A Study of LoRa Long Range Low Power Networks for the Internet of Things.Of all these headers, the FCnt field is of particular importance in providing the frame counter, used as an IV for the encryption of the FRMPayload. This allows for classifying the frames based on their counter (FCnt) and the device (DevAddr) from which they come.
If the device is restarted (either because the battery is exhausted, because it no longer receives sunlight, or in the case of a battery charged by the solar panel, the battery is worn out), the meters will return to 0 and the keystream will be restarted. If the ABP activation keys have not been changed after several meter resets (say, every morning when the solar panel is feeding the panel again), the rated frames could look like this:
FCnt: 0000
FRMPayload: e6 9c 90 93
FRMPayload: e6 9c 90 fd
FRMPayload: e6 9c 90 f5
FRMPayload: e6 9c 90 de
FCnt: 0001
FRMPayload: b2 e1 27 4c
FRMPayload: b2 e1 27 3c
FRMPayload: b2 e1 27 36
FRMPayload: b2 e1 27 2b
FCnt: 0002
FRMPayload: c0 bd cb 9b
FRMPayload: c0 bd cb f2
FRMPayload: c0 bd cb e0
FRMPayload: c0 bd cb ff
FCnt: 0003
FRMPayload: 4e cb ed 10
FRMPayload: 4e cb ed 02
FRMPayload: 4e cb ed 6e
FRMPayload: 4e cb ed 39
From this we can deduce several things. Firstly, for the same counter value, the most significant bits of the captures do not seem to change. This is, on the one hand, to be expected as we are reusing the same keystream, and on the other hand, compatible with headers of type Cayenne LPP, in which the first two bytes indicate the channel and the type of data respectively, and therefore they will not change either. The last two bytes then correspond to the data to be transmitted, which also suggests a 16-bit integer and big endian as more variability is observed in the rightmost byte.
Traditional attacks on CTR mode encryption with keystream reuse are based on applying known plain-text crib dragging, or applying different types of correlations. In this case such a thing is not so easy: the data may possibly come from a sensor, may be numerical values in any range and may be affected by noise. Even so, and because it is a sensor, we can exploit a property of this data to break some bits of the key: a sensor (be it of temperature, humidity, water level, etc.) does not expect extremely abrupt changes between consecutive measurements, beyond the noise.
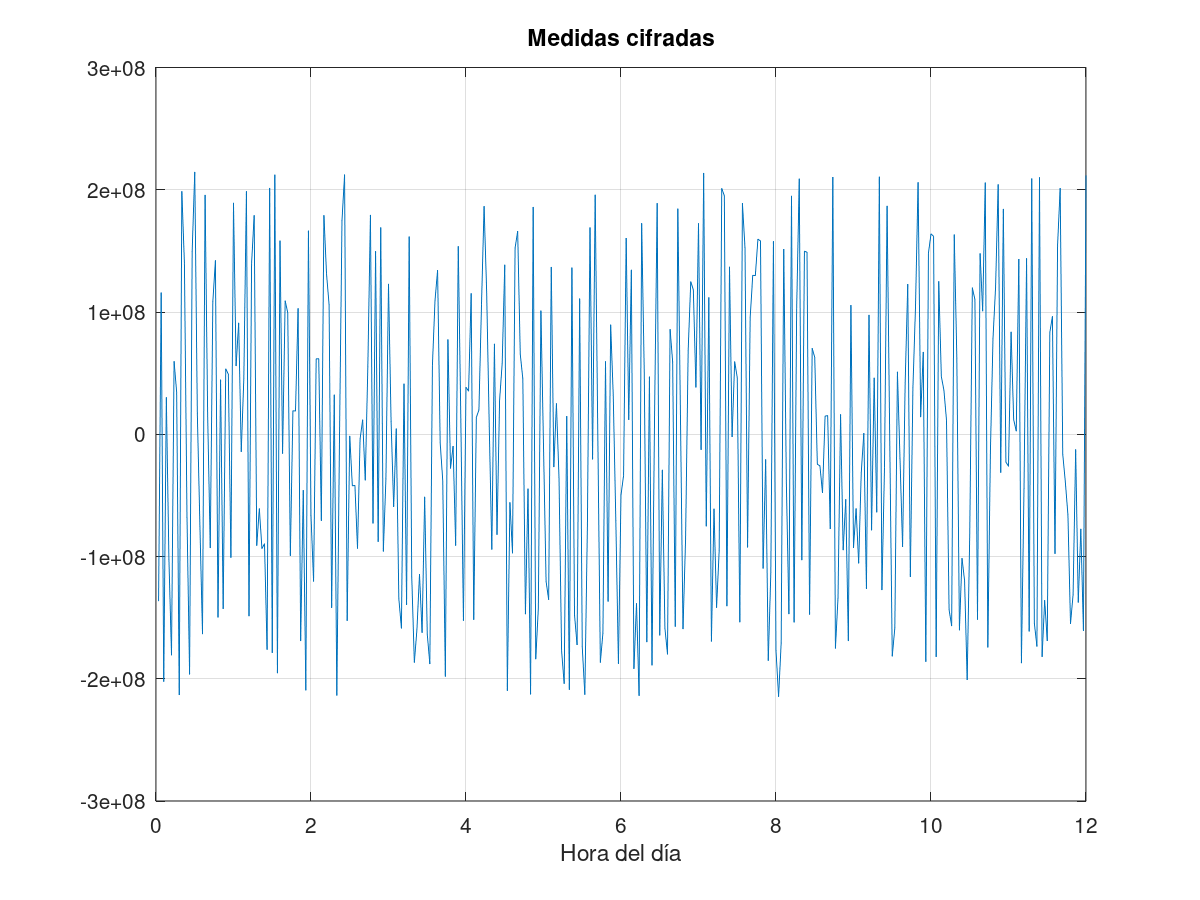
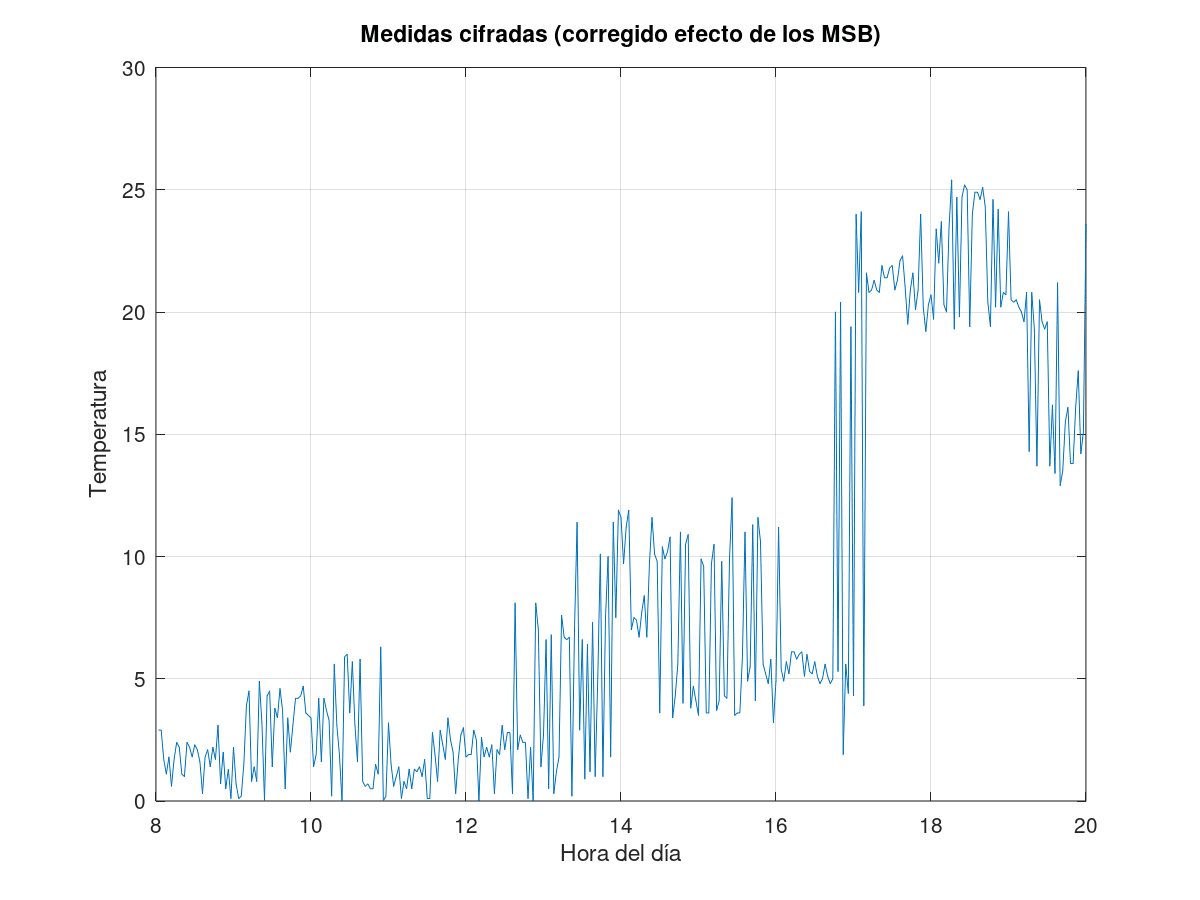
This is justified by the nature of these magnitudes (for example, if the temperature is taken every minute, it is very unlikely that it is randomly varying between 0 and 100 degrees from one measurement to the next). Similarly, if you represent the 32 bits of the encrypted frames as integers over a series of observations on a graph, you will get something like this:
That is, a signal with a dispersion of about 4·109 units (approximately the range of values covered by a 32-bit integer), something fundamentally different from what is expected from a magnitude such as temperature, GPS coordinates, or air humidity.
In a first (naive) approximation to the problem, you can compare the bits of the frames of different days but with the same counter and estimate the probability that they are one or zero based on these comparisons. Bits that are always 0 or 1 will have a probability of 1, while bits that experience some variation (the rightmost bits) will have an intermediate probability between 0 and 1. By composing a temporary key stream with zeros or ones depending on the bit probability, we eliminate the effects of the key on the most significant but less variable bits. It is important to note that this first key stream need not look at all like the original: it will simply serve to override the bits that change the least and to better observe the encrypted bits into which the actual information is encoded.
For this proof of concept, it will be assumed that the device is sending temperature measurements, although in principle we would not have to know what kind of magnitude it is beyond that of a sensor measurement. By applying this pseudo-keystream to the coded measurements, much of the observed variability disappears, and a graph like the one below is drawn:
This suggests that only about 5 bits of the measurements are varying (since the values are between 0 and 25, and the smallest value observed is 1). These are the bits of the key stream that can potentially be found in each frame.
Although in principle we do not know the real value of these bits, the following working hypothesis can be applied: the variation of the measurements over time is smooth, so the absolute value of the derivative of the measurements deciphered over the day should be small. This is the opposite of what can be observed with encrypted measurements, even eliminating the effect of the MSB bits (see above), where the variability is too great. This encourages reformulating the attack to this data as a gradient-free optimization problem: the key is a set of bits such that, if applied by means of XOR to the encrypted measurements, minimizes a cost function given by the absolute value of the derivatives of the decrypted measurements:
Where Si are the set of 32-bit integers that make up the stream of some key stream, Ki the candidate key stream, and Cij the set of encrypted measures after removing the effects of the least variable bits over a day and several days (for example C23 would represent the encrypted measurement within the frame with FCnt 2 on day 3 starting at 0).
The cost function U(Si, Cij) is simply a measure of the dispersion of the derivatives of the Cij curves after applying an XOR with the Si keystream:
With N the number of days in which a traffic observation was made with a counter reset, and M the number of frames captured each day.
The implementation of the optimizer can be done in several ways. A simulated annealing has been chosen for this test because of its simplicity, although there may be better alternatives. The implementation of the proof of concept simulates a set of temperature measurements (360) over several days (100) that vary smoothly with different amplitudes, delays, means and uncertainties:
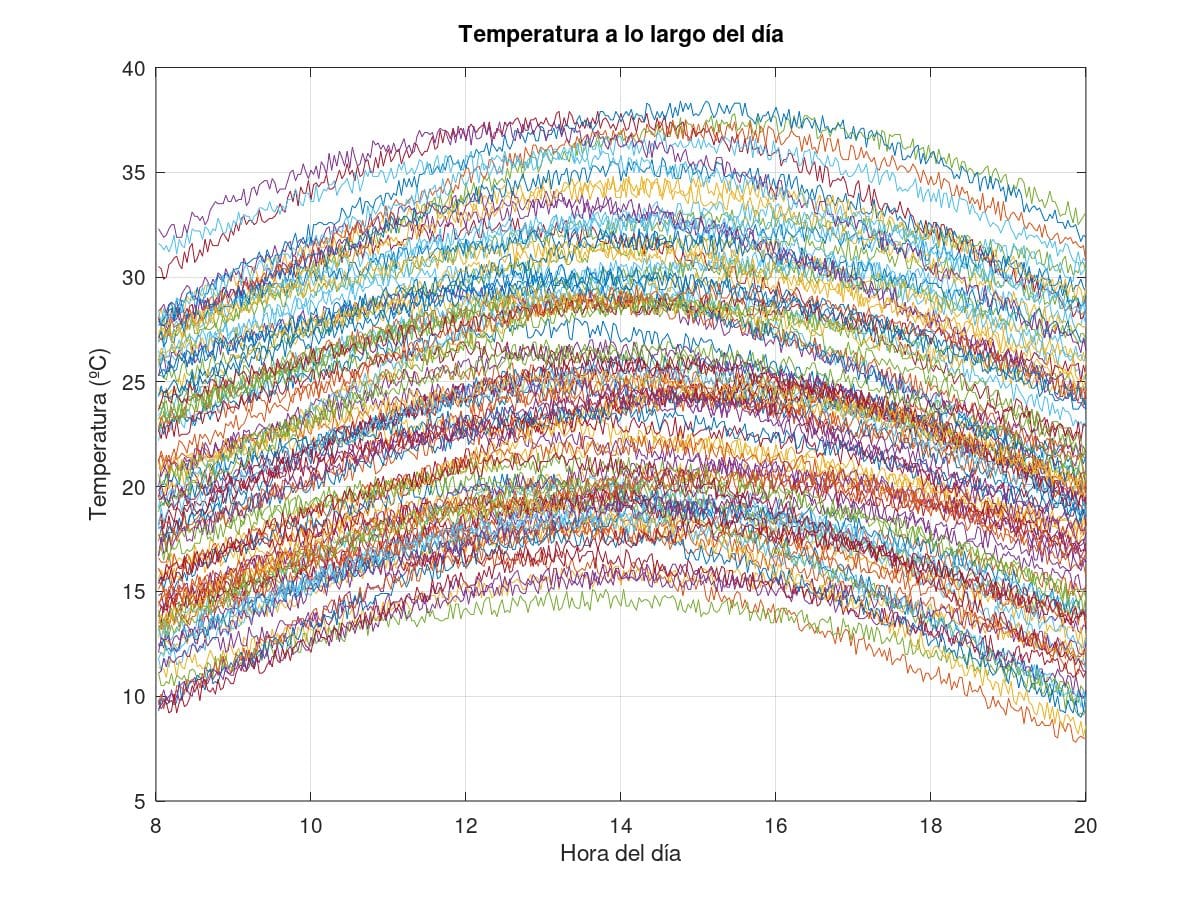 Simulated temperature measurements over 100 days. Each curve represents the change in temperature over the course of a day.
Simulated temperature measurements over 100 days. Each curve represents the change in temperature over the course of a day.It then figures them with the same random keystream and applies the optimizer described above. It has been possible to verify that, if the measurements made over different days are sufficiently different, this technique is capable of recovering the original measurements, with all the error condensed in the least significant bit of the measurements:
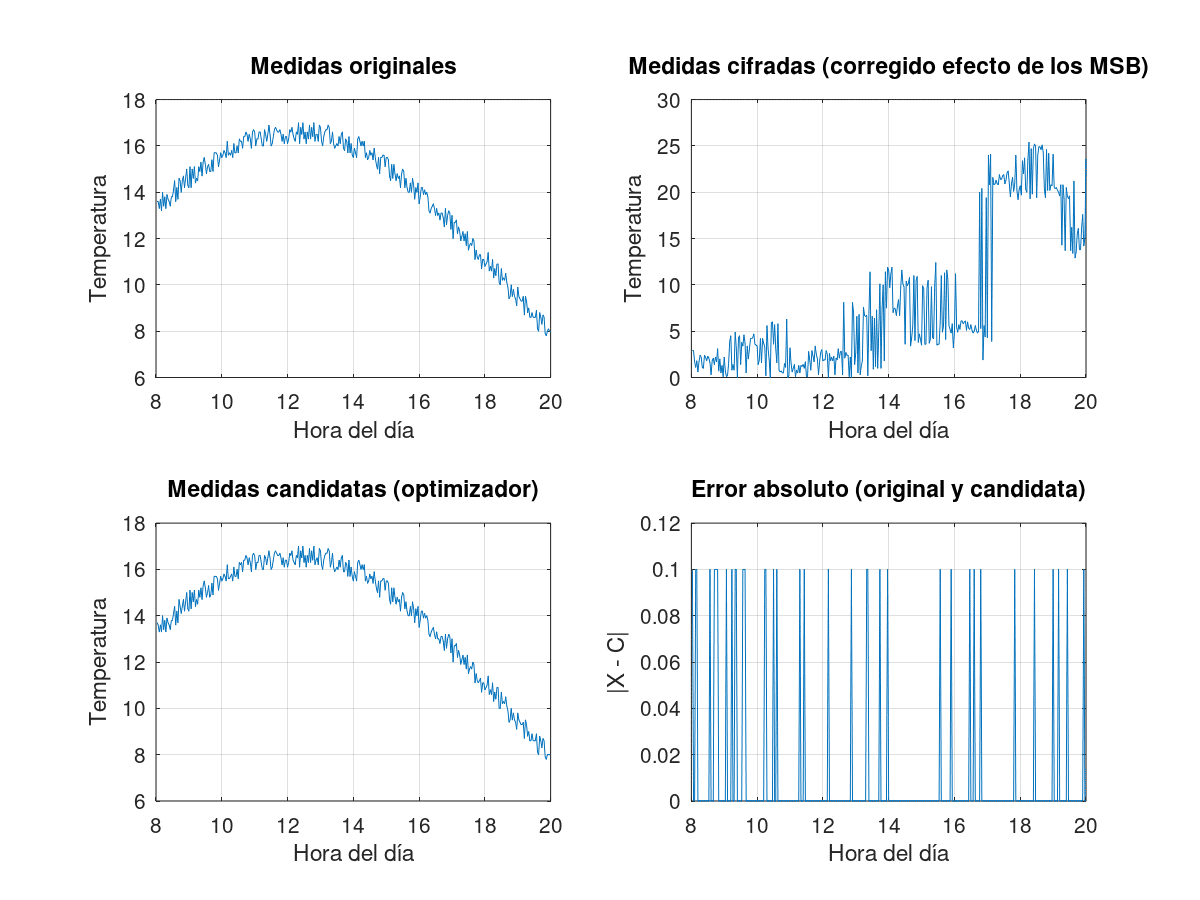 Results of this technique, from left to right and from top to bottom: 1) original measurements, uncoded. 2) Measures in figures, after correction for the effect of the less variable MSBs 3) Candidate measures, at the output of the optimiser. 4) Absolute error, compared as the difference between encrypted and decrypted measurements.
Results of this technique, from left to right and from top to bottom: 1) original measurements, uncoded. 2) Measures in figures, after correction for the effect of the less variable MSBs 3) Candidate measures, at the output of the optimiser. 4) Absolute error, compared as the difference between encrypted and decrypted measurements.Conclusions
The threats to the confidentiality of LoRaWAN 1.0 communications are not merely theoretical: the smooth nature of the sensor data can seriously compromise the confidentiality of transmissions and therefore the keystream. Although the attack presented above is quite simple and looks too much like a correlation attack (as it exploits the regularity of the original data with respect to the ciphers), the author has been unable to find references to this particular technique in the literature. Any article, manual or publication in which it is described in depth is welcome.
We take this opportunity to thank Alfonso Muñoz for his insight into the pros and cons of this attack.
Discover our work and cybersecurity services at www.tarlogic.com
This article is part of a series of articles about LoRaWAN
- Cybersecurity in LoRa and LoRaWAN: Context and Background
- LoRaWAN 1.0, vulnerabilities and backward compatibility in version 1.1